Python + numpyを使って、3次元球面上/球内にランダムに点を描画するプログラム

原理は先人のページを参考にしてほしい。以下、3次元球面上に乱数で点を描画するプログラムのPythonによる実装

import numpy as np
xs = []
ys = []
zs = []

# 乱数を初期化
rng = np.random.RandomState(123)
for _ in range(5000):
    theta = np.arccos(rng.uniform(-1, 1))
    phi = rng.uniform(0, 2*np.pi)
    x = np.sin(theta) * np.cos(phi)
    y = np.sin(theta) * np.sin(phi)
    z = np.cos(theta)
    xs.append(x)
    ys.append(y)
    zs.append(z)
    
#以下描画用
import matplotlib.pyplot as plt

plt.hist(xs,bins=30)
plt.show()
plt.hist(ys,bins=30)
plt.show()
plt.hist(zs,bins=30)
plt.show()
plt.scatter(xs,ys,marker=".")
plt.show()
plt.scatter(ys,zs,marker=".")
plt.show()
plt.scatter(zs,xs,marker=".")
plt.show()

出力されたグラフの一部

f:id:onsanai:20200701230510p:plain:w400

3次元球内に乱数で点を描画するプログラムは、for文を以下のように変更する

for _ in range(5000):
    theta = rng.uniform(-1,1)
    phi = rng.uniform(0,2*np.pi)
    r = rng.uniform(0, 1)
    x=r**(1/3)*(1-theta**2)*np.cos(phi)
    y=r**(1/3)*(1-theta**2)*np.sin(phi)
    z=r**(1/3)*theta
    xs.append(x)
    ys.append(y)
    zs.append(z)

出力されたグラフの一部

f:id:onsanai:20200701231532p:plain:w400

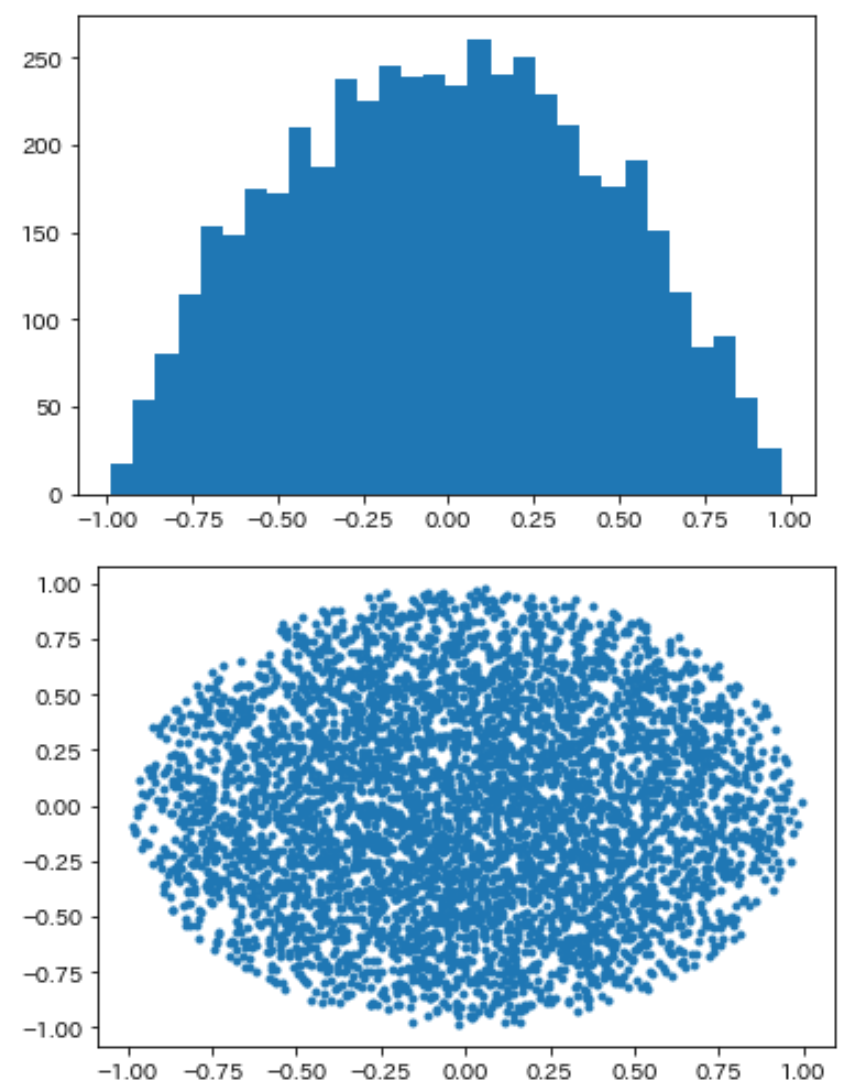
参考までに、円の内部に乱数で点を描画するプログラム

import numpy as np
xs = []
ys = []

# 乱数を初期化
rng = np.random.RandomState(13)
for _ in range(5000):
    phi = rng.uniform(0,2*np.pi)
    r = rng.uniform(0, 1)
    x=r**(1/2)*np.cos(phi)
    y=r**(1/2)*np.sin(phi)
    xs.append(x)
    ys.append(y)