Windows ROOTとPython(numpy,awkward)でTreeファイルの生成と出力時間を比べる

この記事の Awkward のバージョンは1.X.Xです

エマルションの飛跡情報(x,y,ax,ay,ax0,ay0,ax1,ay1)とする。Visual StudioでコンパイルしたROOTと、Python+numpy,awkwardで作ったバージョンを比較する。イベント数は1億(10⁸)本とする。

Visual Studio でコンパイルしたROOT版。248秒もかかった。

#include <TFile.h>
#include <TTree.h>
#include <iostream>

#include <random>
#include <chrono>

void writeTreeToFile() {
    TFile* file = new TFile("output.root", "RECREATE");
    TTree* tree = new TTree("tree", "Tree Title");

    double x, y, ax, ay, ax0, ay0, ax1, ay1;

    tree->Branch("x", &x, "x/D");
    tree->Branch("y", &y, "y/D");
    tree->Branch("ax", &ax, "ax/D");
    tree->Branch("ay", &ay, "ay/D");
    tree->Branch("ax0", &ax0, "ax0/D");
    tree->Branch("ay0", &ay0, "ay0/D");
    tree->Branch("ax1", &ax1, "ax1/D");
    tree->Branch("ay1", &ay1, "ay1/D");

    int seed = 0;
    std::mt19937 gen(seed);
    std::uniform_real_distribution<double> dist_pos(0, 300);  // 一様分布 位置 mm
    std::uniform_real_distribution<double> dist_sn(0, 1);     // 一様分布 SN

    std::normal_distribution<double> dist_ang(0, 0.4);            // 正規分布 角度分布
    std::normal_distribution<double> dist_dang_signal(0, 0.1);    // 正規分布 角度差分布

    // 1億本
    for (int i = 0; i < 1 * 10000 * 10000; i++) {
        x = dist_pos(gen);
        y = dist_pos(gen);
        ax = dist_ang(gen);
        ay = dist_ang(gen);
        if (dist_sn(gen) < 0.2) {
            //シグナル成分
            ax0 = ax + dist_dang_signal(gen);
            ay0 = ay + dist_dang_signal(gen);
            ax1 = ax + dist_dang_signal(gen);
            ay1 = ay + dist_dang_signal(gen);
        }
        else {
            //ノイズ成分
            ax0 = ax + dist_dang_signal(gen) * 5;
            ay0 = ay + dist_dang_signal(gen) * 5;
            ax1 = ax + dist_dang_signal(gen) * 5;
            ay1 = ay + dist_dang_signal(gen) * 5;
        }

        tree->Fill();
    }

    tree->Write();

    file->Close();
    delete file;
}

int main() {
    auto start = std::chrono::system_clock::now();   //開始時間
    writeTreeToFile();
    auto end = std::chrono::system_clock::now(); //終了時間

    std::cout << std::chrono::duration_cast<std::chrono::milliseconds>(end - start).count() << " [msec]" << std::endl;
    return 0;
}

次にPython+numpy,awkward版。31秒 (C++の8分の1)で終わった。

import awkward as ak
import numpy as np
import time

start = time.time()

seed=0
rs = np.random.RandomState(seed)

N = 1 * 10000 * 10000
tree = ak.Array({})
tree["x"] = rs.uniform(0,300,N)
tree["y"] = rs.uniform(0,300,N)
tree["ax"] = rs.normal(0,0.4,N)
tree["ay"] = rs.normal(0,0.4,N)
tree["SN"] = rs.uniform(0,1,N)<0.2

diff_sigma = ak.where(tree["SN"], 0.1, 0.5)

tree["ax0"] = tree["ax"] + rs.normal(0,1,N)*diff_sigma
tree["ay0"] = tree["ay"] + rs.normal(0,1,N)*diff_sigma
tree["ax1"] = tree["ax"] + rs.normal(0,1,N)*diff_sigma
tree["ay1"] = tree["ay"] + rs.normal(0,1,N)*diff_sigma

ak.to_parquet(tree, "tree.parquet")

end = time.time()
print(f"{(end-start)*1000:.0f} [msec]")

グラフも作っておく

位置分布

import matplotlib.pyplot as plt
plt.hist2d(tree["x"],tree["y"],bins=[300,300],range=[[0,300],[0,300]])
plt.show()

角度分布

plt.hist2d(tree["ax"],tree["ay"],bins=[300,300],range=[[-1.5,1.5],[-1.5,1.5]])
plt.show()

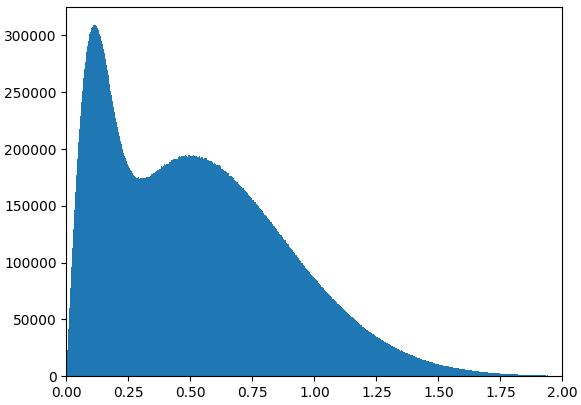
角度差分布

plt.hist(((tree["ax1"]-tree["ax"])**2+(tree["ay1"]-tree["ay"])**2)**0.5,bins=1000,range=[0,2])
plt.xlim(0,2)
plt.show()