の続き
lmfitは、複数の2次元正規分布でもフィッティングができる
gauss = lmfit.models.Gaussian2dModel(prefix="g1") params = gauss.make_params() model = gauss gauss = lmfit.models.Gaussian2dModel(prefix="g2") params.update(gauss.make_params()) model = model+gauss
パラメータに拘束条件をつけることもできる。
これは、g2sigmax = g1sigmax 、 g2sigmay = g1sigmay の意味。
params["g2sigmax"].set(expr="g1sigmax") params["g2sigmay"].set(expr="g1sigmay")
コード全体
import numpy as np import lmfit from lmfit.lineshapes import gaussian2d, lorentzian np.random.seed(0) x0 = np.random.randn(10000)*0.5 + 4 #標準偏差0.5, 平均4の正規分布 y0 = np.random.randn(10000)*2 + 3 #標準偏差2.0, 平均3の正規分布 x1 = np.random.randn(1000)*0.5 + 0 #標準偏差0.5, 平均0の正規分布 y1 = np.random.randn(1000)*2 + 0 #標準偏差2.0, 平均0の正規分布 x=np.concatenate((x0,x1)) y=np.concatenate((y0,y1)) xrange=[-10,10] yrange=[-10,10] bins=[50,100] hist, edgesx, edgesy = np.histogram2d(x,y,bins=bins,range=[xrange,yrange]) arr_x = [] arr_y = [] arr_z = [] arr_zerror = [] for ix,vx in enumerate((edgesx[:-1]+edgesx[1:])*0.5): for iy,vy in enumerate((edgesy[:-1]+edgesy[1:])*0.5): if hist[ix,iy]==0:continue arr_x.append(vx) arr_y.append(vy) arr_z.append(hist[ix,iy]) arr_zerror.append(hist[ix,iy]**0.5) arr_zerror = np.array(arr_zerror) gauss = lmfit.models.Gaussian2dModel(prefix="g1") params = gauss.make_params() model = gauss gauss = lmfit.models.Gaussian2dModel(prefix="g2") params.update(gauss.make_params()) model = model+gauss params["g1centerx"].set(value=3.5,max=5,min=2) params["g1centery"].set(value=1.9,max=3,min=1) params["g1sigmax"].set(value=0.2) params["g1sigmay"].set(value=2) params["g2centerx"].set(value=-0.1,max=0.5,min=-0.5) params["g2centery"].set(value=-0.1,max=0.5,min=-0.5) params["g2sigmax"].set(expr="g1sigmax") params["g2sigmay"].set(expr="g1sigmay") #楕円の点列作成 def get_ellipse_xy(centerx, sigmax, centery, sigmay): t = np.linspace(0, 2*np.pi, 100) x = sigmax*2 * np.cos(t) y = sigmay*2 * np.sin(t) return x+centerx, y+centery import matplotlib.pyplot as plt import matplotlib #初期値のグラフを描く plt.hist2d(x,y,bins=bins,range=[xrange,yrange], norm=matplotlib.colors.LogNorm()) for prefix in ["g1","g2"]: plt.plot(*get_ellipse_xy(*[params[prefix+mem].value for mem in ['centerx','sigmax','centery','sigmay']]),color="tab:red") plt.show() #フィッティング result = model.fit(arr_z, x=arr_x, y=arr_y, params=params, weights=1.0/arr_zerror, scale_covar=False) lmfit.report_fit(result) #フィット後のグラフを描く plt.hist2d(x,y,bins=bins,range=[xrange,yrange], norm=matplotlib.colors.LogNorm()) for prefix in ["g1","g2"]: plt.plot(*get_ellipse_xy(*[result.result.params[prefix+mem].value for mem in ['centerx','sigmax','centery','sigmay']]),color="tab:red") plt.show()
結果
図中の楕円は2σのライン
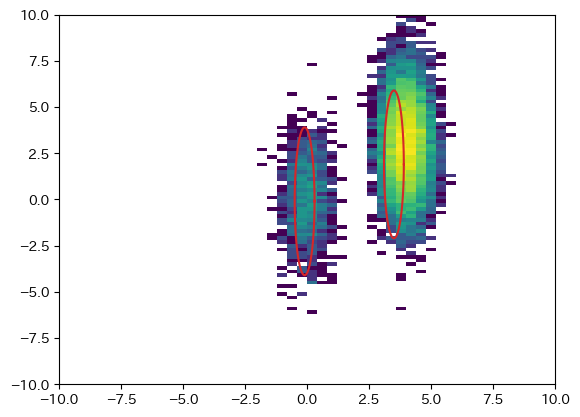
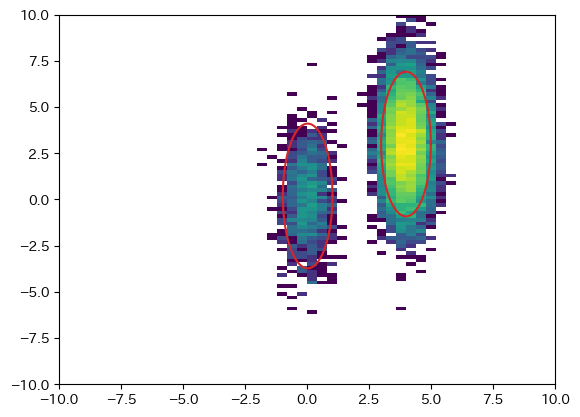
[[Fit Statistics]]
# fitting method = leastsq
# function evals = 161
# data points = 679
# variables = 8
chi-square = 568.042626
reduced chi-square = 0.84656129
Akaike info crit = -105.150348
Bayesian info crit = -68.9853788
[[Variables]]
g1amplitude: 774.765317 +/- 7.90402876 (1.02%) (init = 1)
g1centerx: 3.98680648 +/- 0.00516811 (0.13%) (init = 3.5)
g1centery: 3.00000000 +/- 4.4017e-05 (0.00%) (init = 1.9)
g1sigmax: 0.50043538 +/- 0.00374820 (0.75%) (init = 0.2)
g1sigmay: 1.95719965 +/- 0.01511816 (0.77%) (init = 2)
g1fwhmx: 1.17843524 +/- 0.00882635 (0.75%) == '2.3548200*g1sigmax'
g1fwhmy: 4.60885287 +/- 0.03560055 (0.77%) == '2.3548200*g1sigmay'
g1height: 1242.53007 +/- 18.3067883 (1.47%) == '1.5707963*g1amplitude/(max(1e-15, g1sigmax)*max(1e-15, g1sigmay))'
g2amplitude: 69.4744491 +/- 2.44157021 (3.51%) (init = 1)
g2centerx: 0.02245085 +/- 0.01950439 (86.88%) (init = -0.1)
g2centery: 0.19129074 +/- 0.07640330 (39.94%) (init = -0.1)
g2sigmax: 0.50043538 +/- 0.00374820 (0.75%) == 'g1sigmax'
g2sigmay: 1.95719965 +/- 0.01511816 (0.77%) == 'g1sigmay'
g2fwhmx: 1.17843524 +/- 0.00000000 (0.00%) == '2.3548200*g2sigmax'
g2fwhmy: 4.60885287 +/- 0.00000000 (0.00%) == '2.3548200*g2sigmay'
g2height: 111.419665 +/- 3.91566886 (3.51%) == '1.5707963*g2amplitude/(max(1e-15, g2sigmax)*max(1e-15, g2sigmay))'
確かに、g1sigmaxとg2sigmax、g1sigmaxとg2sigmayのフィット結果は同じになっている。