Python: 重イオンのEnergy loss と Energy loss straggling - 物理の駅 Physics station by 現役研究者

まず、各定数の確認する。

import numpy as np

elementary_charge = 1.602176634*10**-19 # 電気素量 C
c_light_m = 299792458 # 光速 m/s
electron_mass_kg = 9.1093837015*10**-31 # 電子質量 kg
permittivity_vacuum = 8.8541878128*10**-12 # 真空の誘電率 F/m = C/Vm
r_e = 2.8179403262*10**-13 #古典電子半径 cm
print("r_e =", elementary_charge**2 / (4 * np.pi * permittivity_vacuum * electron_mass_kg * c_light_m**2)*100,"cm")

electron_mass = 0.510998928 #   // 電子質量 MeV/c^2
Na = 6.02214179*10**23 # アボガドロ数 /mol
dedx_constant = 0.3070749187 #4*pi*Na*me*c^2*r_e^2  //MeV cm^2
print("dedx_constant =", 4 * np.pi * Na * electron_mass * r_e**2,"MeV/cm2")

色んな項を無視したエネルギー損失と、エネルギーストラグリングを計算する。

def energy_loss_straggling(p_A, p_Z, p_Q, p_T, t_Z, shell_correction = False, LSX=1):
    '''
    p_A=238 # projectileのA
    p_Z=92 # projectileのZ
    p_Q=92 # projectileのQ
    p_T = 345 #projectileのEnergy MeV/u
    t_Z = 4       # tagetのZ
    '''
    import numpy as np

    electron_mass = 0.510998928 #   // 電子質量 MeV/c^2
    Na = 6.02214179*10**23 # アボガドロ数 /mol
    dedx_constant = 0.3070749187 #4*pi*Na*me*c^2*r_e^2  //MeV cm^2
    atomic_mass_unit = 931.4940954 # // 統一原子質量単位 MeV/c^2

    zp_eff = p_Q #projectileのQ
    gamma=1.0 + p_T/atomic_mass_unit
    beta2=1.0-1.0/(gamma*gamma)
    beta = np.sqrt(beta2)

    def get_a(t_Z):
        standard_weights = [1.008, 4.003,\
            6.941, 9.012, 10.81, 12.01, 14.01, 16.00, 19.00, 20.18,\
            22.99, 24.31, 26.98, 28.09, 30.97, 32.07, 35.45, 39.95,\
            39.10, 40.08, 44.96, 47.87, 50.94, 52.00, 54.94, 55.85, 58.93, 58.69, 63.55, 65.38, 69.72, 72.63, 74.92, 78.97, 79.90, 83.80,\
            85.47, 87.62, 88.91, 91.22, 92.91, 95.95, 99, 101.1, 102.9, 106.4, 107.9, 112.4, 114.8, 118.7, 121.8, 127.6, 126.9, 131.3,\
            132.9, 137.3,\
            138.9, 140.1, 140.9, 144.2, 145, 150.4, 152.0, 157.3, 158.9, 162.5, 164.9, 167.3, 168.9, 173.0, 175.0,\
            178.5, 180.9, 183.8, 186.2, 190.2, 192.2, 195.1, 197.0, 200.6, 204.4, 207.2, 209.0, 210, 210, 222,\
            223, 226,\
            227, 232.0, 231.0, 238.0, 237, 239, 243, 247, 247, 252, 252, 257, 258, 259, 262,\
            267, 268, 271, 272, 277, 276, 281, 280, 285, 278, 289, 289, 293, 293, 294]
        return standard_weights[t_Z-1]

    t_A = get_a(t_Z)

    def get_ipot(t_Z):
        arr_ipot = [
            19.2, 41.8, \
            40.0, 63.7, 76.0, 81.0, 82.0, 95.0, 115.0,137.0,\
            149.0,156.0,166.0,173.0,173.0,180.0,174.0,188.0,\
            190.0,191.0,216.0,233.0,245.0,257.0,272.0,286.0,297.0,311.0,322.0,330.0,334.0,350.0,347.0,348.0,343.0,352.0,\
            363.0,366.0,379.0,393.0,417.0,424.0,428.0,441.0,449.0,470.0,470.0,469.0,488.0,488.0,487.0,485.0,491.0,482.0,\
            488.0,491.0,501.0,523.0,535.0,546.0,560.0,574.0,580.0,591.0,614.0,628.0,650.0,658.0,674.0,684.0,694.0,705.0,718.0,727.0,736.0,746.0,757.0,790.0,790.0,800.0,810.0,823.0,823.0,830.0,825.0,794.0,\
            827.0,826.0,841.0,847.0,878.0,890.0,900.0,910.0,920.0,930.0,940.0,950.0,960.0,970.0,980.0,990.0,1000.,1010.,1020.,1030.,1040.,1050.,1060.,1070.,1080.,1090.,1100.,1110.,1120.,1130.,1140.,1150.
            ]
        return arr_ipot[t_Z-1]
    Ipot = get_ipot(t_Z) #平均イオン化ポテンシャル [eV]
    
    f1 = dedx_constant*pow(zp_eff,2.0)*t_Z/(beta2*t_A)
    f2 = np.log(2.0*electron_mass*beta2*gamma*gamma/(Ipot/1000000)) - beta2
    
    cor = 0 #shell補正
    f2 = f2 - cor/t_Z 

    barkas = 1.0 #barkas補正
    LS = 0.0     #LS補正
    delta = 0    #密度補正

    energy_loss  = ((f2)*barkas + LS - delta/2.)*f1 #補正なしのEnergy loss MeV/(g/cm2)
    energy_straggling = f1 * electron_mass * beta2 * gamma * gamma * LSX #Energy straggling  MeV^2/(g/cm2)
    
    return energy_loss, energy_straggling

dedxの定数 dedx_constant=Kを次式のように定義すると、

$\displaystyle K=4\pi N_A r_e^2 m_e c^2$

諸々の補正項を無視するとdE/dxは次式のように表現される。

$\displaystyle \frac{dE}{dx} = K Z_p^2 \frac{Z_t}{A_t}\frac{1}{\beta^2} \left(\ln \left(\frac{2m_e \beta^2 \gamma^2}{I} \right) - \beta^2\right)$

energy loss straggling Ωは次式のように表現される。

$\displaystyle \frac{d\Omega^2}{dx} = K Z_p^2 \frac{Z_t}{A_t}\frac{1}{\beta^2} m_e \beta^2 \gamma^2 X$

345MeV/uの238U、320MeV/uの4Heを、ベリリウムの薄膜に入射したした場合の計算。

print(energy_loss_straggling(p_A=238, p_Z=92, p_Q=92, p_T=345, t_Z=4))
print(energy_loss_straggling(p_A=4, p_Z=2, p_Q=2, p_T=320, t_Z=4))

(22419.411135356077, 1107.0218819306313)
(11.02602078859991, 0.5028755625661142)

と返ってくるはずである。

標的をBe1mmとすると、物質量0.185 g/cm2をかければ、Energy loss と stragglingの2乗の値が得られる。345MeV/uの238U92+ビームのEnergy lossは 4147.6 MeV、Energy stragglingは14.3 MeVとなる。それぞれAで割ると、Energy lossは17.43±0.06 MeV/uとなる。LISE++で出力される値は17.85±0.08 MeV/uである。

320MeV の 4HeビームがBe標的1mmに入射したとき、Energy lossは2.04 MeV、Energy stragglingは0.31 MeVである。それぞれAで割ると、Energy lossは0.510±0.076 MeV/uとなる。LISE++の値は0.508±0.068 MeV/uである。

精度よくEnergy lossを求めるためには、barkas項、delta項、LS項を与える必要がある。

stragglingにかけるべきXの値はATIMAで計算でき、それを与えるとLISE++の値とほぼ一致する。

よくあるStopping powerの図を描く。粒子は陽子、標的は銅(Z=29)にして、横軸はβγにした。

import matplotlib.pyplot as plt
import numpy as np
elosses = []
betagammas = []
for log_energy in range(-10,50):
    energy = 10**(log_energy*0.1)
    eloss, strag = energy_loss_straggling(p_A=1, p_Z=1, p_Q=1, p_T=energy, t_Z=29)
    atomic_mass_unit = 931.4940954 # // 統一原子質量単位 MeV/c^2
    gamma=1.0 + energy/atomic_mass_unit
    beta2=1.0-1.0/(gamma*gamma)
    beta = np.sqrt(beta2)
    betagammas.append(beta*gamma)
    elosses.append(eloss)
plt.rcParams["font.size"] = 14
plt.rcParams['figure.figsize'] = [7, 5]
plt.plot(betagammas,elosses)
plt.xscale("log")
plt.yscale("log")
plt.ylim(1,None)
plt.xlabel("βγ")
plt.ylabel("MeV / (g/cm2)")
plt.show()

PDGの2018年版ブックレットの図33.1と比較する。

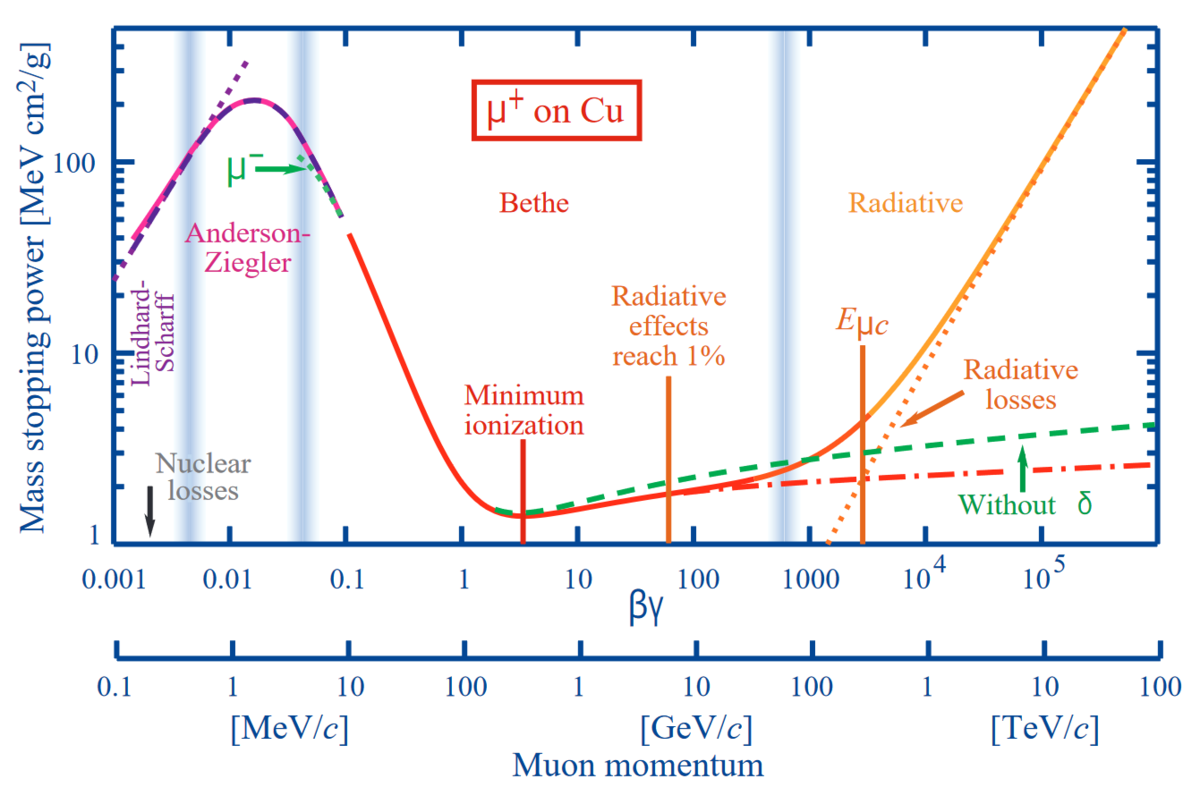
概ね問題なさそうだ。

密度補正deltaの部分は比較的簡単にPythonで書けた

def bethek_density_effect(beta, t_Z, beta, gamma):
    '''
    密度効果補正
    '''
    del_0= [
    0.0,  0.00,  0.14, 0.14, 0.14, 0.12, 0.00, 0.00, 0.00, 0.00,
    0.08, 0.08,  0.12, 0.14, 0.14, 0.14, 0.00, 0.00, 0.10, 0.14,
    0.10, 0.12,  0.14, 0.14, 0.14, 0.12, 0.12, 0.10, 0.08, 0.08,
    0.14, 0.14,  0.08, 0.10, 0.00, 0.00, 0.14, 0.14, 0.14, 0.14,
    0.14, 0.14,  0.14, 0.14, 0.14, 0.14, 0.14, 0.14, 0.14, 0.14,
    0.14, 0.14,  0.00, 0.00, 0.14, 0.14, 0.14, 0.14, 0.14, 0.14,
    0.14, 0.14,  0.14, 0.14, 0.14, 0.14, 0.14, 0.14, 0.14, 0.14,
    0.14, 0.14,  0.14, 0.14, 0.08, 0.10, 0.10, 0.12, 0.14, 0.14,
    0.14, 0.14,  0.14, 0.14, 0.00, 0.00, 0.00, 0.14, 0.14, 0.14,
    0.14, 0.14,  0.14, 0.14, 0.14, 0.14, 0.14 ]
    x0= [
    1.8639, 2.2017,  0.1304, 0.0592, 0.0305, -.0178, 1.7378, 1.7541, 1.8433, 2.0735,
    0.2880, 0.1499,  0.1708, 0.2014, 0.1696, 0.1580, 1.5555, 1.7635, 0.3851, 0.3228,
    0.1640, 0.0957,  0.0691, 0.0340, 0.0447, -.0012, -.0187, -.0566, -.0254, 0.0049,
    0.2267, 0.3376,  0.1767, 0.2258, 1.5262, 1.7158, 0.5737, 0.4585, 0.3608, 0.2957,
    0.1785, 0.2267,  0.0949, 0.0599, 0.0576, 0.0563, 0.0657, 0.1281, 0.2406, 0.2879,
    0.3189, 0.3296,  0.0549, 1.5630, 0.5473, 0.4190, 0.3161, 0.2713, 0.2333, 0.1984,
    0.1627, 0.1520,  0.1888, 0.1058, 0.0947, 0.0822, 0.0761, 0.0648, 0.0812, 0.1199,
    0.1560, 0.1965,  0.2117, 0.2167, 0.0559, 0.0891, 0.0819, 0.1484, 0.2021, 0.2756,
    0.3491, 0.3776,  0.4152, 0.4267, 0.4300, 1.5368, 0.6000, 0.5991, 0.4559, 0.4202,
    0.3144, 0.2260,  0.1869, 0.1557, 0.2274, 0.2484, 0.2378]
    gamma = 1/np.sqrt(1-(beta*beta))
    x = np.log(beta * gamma) / 2.3025851
    delta = del_0[t_Z-1] * pow(10.0,(2.*(x-x0[t_Z-1])))
    return delta

全てのコードのまとめ

gitlab.com

参照: C++のCATIMAコード