PyROOTでROOTファイルを読む TFileとRDataFrameの比較

PyROOTでROOTファイルを扱うには、ROOTの作法に従うか、Numpyで頑張るかの2択となる。

ROOTの作法に従った例

ROOTファイルに、イベントごとに色んなパラメータが固定長で格納されているものとする。データ名 ADC の[0]に格納されているデータをヒストグラムで表示する。

import ROOT
file = ROOT.TFile.Open("filename.root")
tree = file.Get('tree')
c1 = ROOT.TCanvas("c1","c1",800,500)
h1 = ROOT.TH1I("h1", "h1", 150, 7000, 10000)
tree.Draw("ADC[0]>>h1")
c1.Draw()

描画するだけなら楽。

次、Numpyオブジェクトにしてからmatplotlibで描画する。

import ROOT
import numpy as np
import matplotlib.pyplot as plt
df = ROOT.RDataFrame("tree", "filename.root")
npy = df.AsNumpy()
plt.hist([a[0] for a in npy["ADC"]],range=[7000,10000],bins=150)
plt.show()

データの扱いがめんどくさいが、グラフの扱いは楽。数値計算をもっと便利にできるライブラリもあるとは思うが、僕は知らない。

データを加工したり、カットをかけたりする場合は、やはりROOTで頑張ったほうが楽だな、と。

例えば、ADC[0]が9000以上を、ADCの[0]と[1]の相乗平均でヒストグラムを描画する。

tree.Draw("(ADC[0]*ADC[1])**(1.0/2.0)>>h1","ADC[0]>9000")
c1.Draw()

上記を正規分布でフィッティングする

tree.Draw("(ADC[0]*ADC[1])**(1.0/2.0)>>h1","ADC[0]>9000")
f1 = ROOT.TF1("f1","gaus",7000,10000)
h1.Fit("f1")
ROOT.gStyle.SetOptFit(1)
c1.Draw()

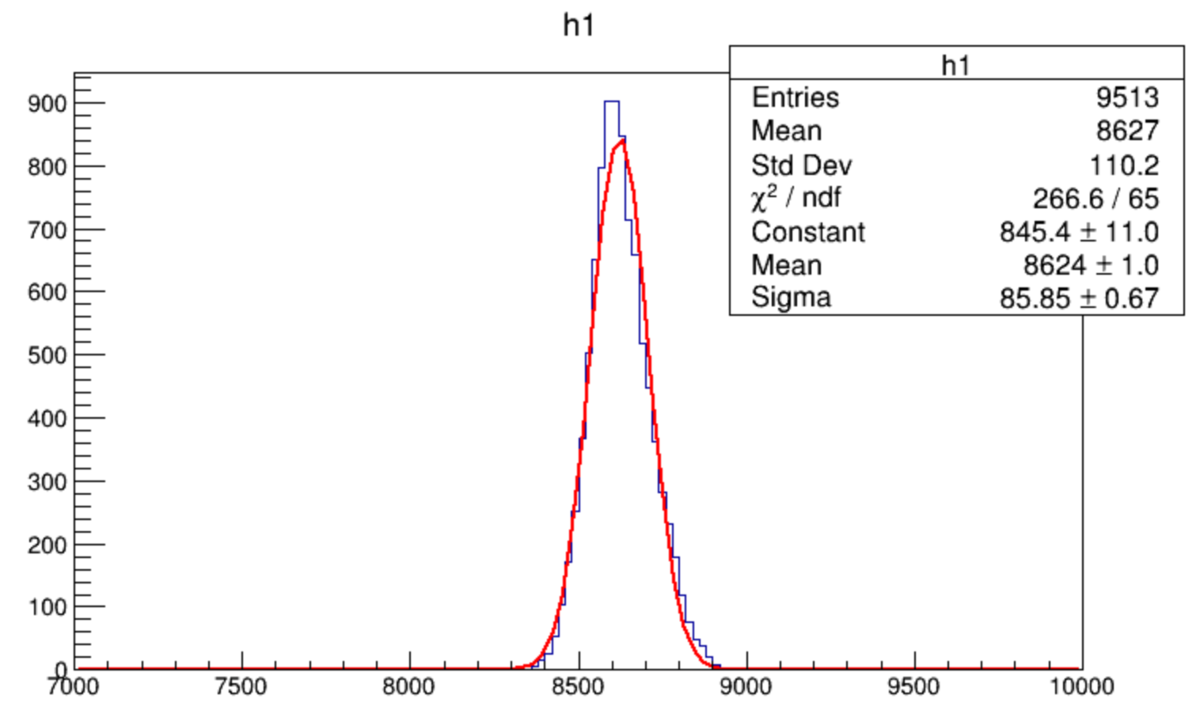
PyROOTになったところでROOTであることは変わらないので、ROOTの作法を覚える手間はほぼ変わらないので、ROOT C++でいいじゃんって思う。

仮に、Pythonで容易にデータ解析ができるフレームワークを持っている実験グループは、ROOTが内部でゴリゴリC++で実装しているように、誰かが裏でゴリゴリコーディングしてくれているおかげなのだ、ということを忘れないでほしい。